一 快速排序
快排的基本思想:基于分治
主要思想:
根据给定的所有数,每次取出一个数x作为分界,每次调整区间,使得左边区间的数都小于等于x,右边区间的数都大于等于x。递归处理左右两段。
基本步骤:
1.确定分界点
2.调整区间
3.递归处理
调整区间的两种方法: 暴力和双指针做法。
暴力:多开辟两个数组a,b,先扫描原数组q,小于等于x的存入a,大于x的存入b。最后将ab按顺序存回q。
双指针:不需要额外的空间。指针i从左向右扫描,指针j从右向左扫描。如果i碰到的数小于x那么继续右移,否则停止。j遇到的数大于x那么继续左移,否则停止。当i和j都停止的时候交换i j位置上的数。直到i和j相互穿过停止。
快排算法模板
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| #include<iostream>
#include<algorithm>
using namespace std;
const int N=100010;
int q[N];
int n;
void quick_sort(int q[],int l,int r){
if(l>=r) return;
int x=q[l+r >> 1],i=l-1,j=r+1;
cout<<"the divided number is:"<<x<<endl;
while(i<j){
do i++; while(q[i]<x);
do j--; while(q[j]>x);
if(i<j) swap(q[i],q[j]);
for(int i=0;i<n;i++) printf("%d ",q[i]);
cout<<endl;
}
quick_sort(q,l,j);
quick_sort(q,j+1,r);
}
int main(){
scanf("%d",&n);
for(int i=0;i<n;i++) scanf("%d", &q[i]);
cout<<"out "<<endl;
quick_sort(q,0,n-1);
for(int i=0;i<n;i++) printf("%d ",q[i]);
system("pause");
return 0;
}
|
可以看一下样例输出:
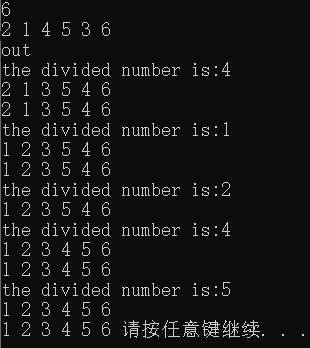
根据输出可以进一步理解,边界x是每一次递归调用时取的。
注意在取x的时候使用的位运算,右移,l+r>>1相当于做的除以2的操作,速度要快很多。
求第k个数
给定一个长度为 n 的整数数列,以及一个整数 k,请用快速选择算法求出数列从小到大排序后的第 k 个数。
输入格式
第一行包含两个整数 n 和 k。
第二行包含 n 个整数(所有整数均在 1∼109 范围内),表示整数数列。
输出格式
输出一个整数,表示数列的第 k 小数。
数据范围
1≤n≤100000,
1≤k≤n
输入样例:
5 3
2 4 1 5 3
输出样例:
3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| #include<iostream>
using namespace std;
const int N=100010;
int q[N];
void quick_sort(int q[],int l,int r){
if(l>=r) return;
int x=q[l+r >> 1],i=l-1,j=r+1;
while(i<j){
do i++;while(q[i]<x);
do j--;while(q[j]>x);
if(i<j) swap(q[i],q[j]);
}
quick_sort(q,l,j);
quick_sort(q,j+1,r);
}
int main(){
int n,m;
scanf("%d%d",&n, &m);
for(int i=0;i<n;i++) scanf("%d",&q[i]);
quick_sort(q,0,n-1);
printf("%d",q[m-1]);
return 0;
}
|
二 归并排序
归并的基本思想:基于分治
基本思想:归并排序和快速排序都是分治的思想,但是不同的是快排取的边界值是要排序的数本身,而归并取得是下标。
步骤:
1.确定分界点 mid=(l+r)/2
2.递归排序左部分和右部分
3.归并,左右两部分合二为一
归并的方法:双指针算法。
假设左右两部分已经排好序了,每次比较left和right的首位置的数,将比较小的数字存到临时数组里面,直到有一部分的数字已经被扫描完。最后将剩余没有扫描的一部分数字直接加到临时数组中。
归并算法模板
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| #include<iostream>
using namespace std;
const int N=100010;
int q[N],temp[N];
int n;
void merge_sort(int q[],int l,int r){
if(l>=r) return;
int mid = l+r >> 1;
merge_sort(q,l,mid),merge_sort(q,mid+1,r);
int k=0;
int i=l,j=mid+1;
while(i<=mid && j<=r){
if(q[i]<=q[j]) temp[k++]=q[i++];
else temp[k++]=q[j++];
}
while(i<=mid) temp[k++]=q[i++];
while(j<=r) temp[k++]=q[j++];
for(int i=l,j=0;i<=r;i++,j++) q[i]=temp[j];
}
int main(){
scanf("%d",&n);
for(int i=0; i<n; i++) scanf("%d",&q[i]);
merge_sort(q,0,n-1);
for(int i=0; i<n; i++) printf("%d ",q[i]);
}
|
求逆序对的数量
给定一个长度为 n 的整数数列,请你计算数列中的逆序对的数量。
逆序对的定义如下:对于数列的第 i 个和第 j 个元素,如果满足 i<j 且 a[i]>a[j],则其为一个逆序对;否则不是。
输入格式
第一行包含整数 n,表示数列的长度。
第二行包含 n 个整数,表示整个数列。
输出格式
输出一个整数,表示逆序对的个数。
数据范围
1≤n≤100000,
数列中的元素的取值范围 [1,109]。
输入样例:
6
2 3 4 5 6 1
输出样例:
5


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| #include<iostream>
using namespace std;
typedef long long LL;
const int N=100010;
int q[N],temp[N];
int n;
LL merge_sort(int q[],int l,int r){
if(l>=r) return 0;
int mid=l+r >> 1;
int i=l,j=mid+1,k=0;
LL res=merge_sort(q,l,mid)+merge_sort(q,mid+1,r);
while(i<=mid&&j<=r){
if(q[i]<=q[j]) temp[k++]=q[i++];
else{
temp[k++]=q[j++];
res+=mid-i+1;
}
}
while(i<=mid) temp[k++]=q[i++];
while(j<=r) temp[k++]=q[j++];
for(int i=l,j=0;i<=r;i++,j++) q[i]=temp[j];
return res;
}
int main(){
scanf("%d",&n);
for(int i=0;i<n;i++) scanf("%d",&q[i]);
cout<<merge_sort(q,0,n-1)<<endl;
}
|
小知识点
1.c++中数据输入很大时,使用scanf读入比cin读入快很多。
2.排序算法的稳定性:指两个数在排序之前和排序之后的相对位置是否变化。
快排不稳定,归并是稳定的。











